Uit TUE
vwo-scheikundemodule 12:
2.1 In het vorige practicum heb je met Lewisstructuren voorspellingen gedaan over en verklaringen gegeven voor de grootte van dipoolmomenten.
a. Leg uit dat “dipoolmoment” een microniveau-eigenschap is.
b. Noem een macroniveau-eigenschap die met (verschil in) dipoolmomenten verklaard kan worden.
Aan de hand van structuurformules of Lewisstructuren kun je ook voorspellen hoeveel isomeren er bestaan bij een bepaalde molecuulformule.
c. Voorspel door het tekenen van Lewisstructuren hoeveel isomeren er zijn met de molecuulformule CH2Cl2.
Het aantal isomeren dat je bij vraag c vindt hangt af van de manier waarop je de H's en Cl's rond de C tekent.
 Hieronder
zie je de twee verschillende structuurformules die je kunt tekenen als je
uitgaat van een zogenaamde "platte” 4-omringing.
Hieronder
zie je de twee verschillende structuurformules die je kunt tekenen als je
uitgaat van een zogenaamde "platte” 4-omringing.
Omdat er maar één stof bestaat met de molecuulformule
CH2Cl2 hebben we destijds gekozen voor de tetraëdrische 4-omringing:
C in het zwaartepunt van een tetraëder (= regelmatig viervlak) met covalente
bindingen naar de H’s op de hoekpunten van die tetraëder:

d. Zie je dat er dan maar één structuurformule te tekenen is?
Vraag, als je dat nodig vindt, om materiaal waarmee je de antwoorden op de vragen c en d kunt controleren.
e. Geef de naam van die ene stof met molecuulformule CH2Cl2.
Meestal wordt zo’n tetraëdrische
structuurformule H
op papier toch zo getekend: I
Cl – C – Cl
Je moet die tetraëder er dan I
zelf bij denken. H
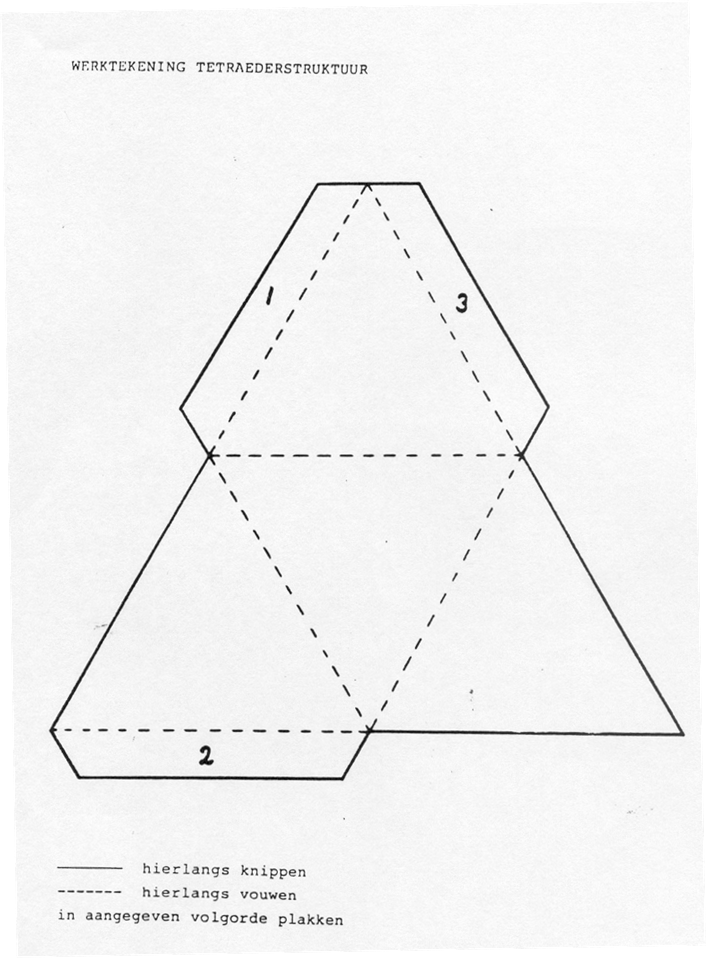
Bouw zelf zo'n tetraëder van papier m.b.v. de werktekening op blz.
2-3w. Bewaar de tetraëder. Je hebt die in een ander practicum nog nodig.
Met zo'n omringing waarbij vier covalente bindingen gericht zijn naar de hoekpunten van een tetraëder kan ook het aantal isomere stoffen met andere molecuulformules dan CH2Cl2 correct voorspeld worden.
f. Geef de namen van de isomere dichloorpropanen.
Je kunt wiskundig bewijzen dat in een tetraëder de hoek
van de verbindingslijnen tussen twee hoekpunten en het zwaartepunt
109,5 ° is.
In de tekening op blz. 2-1 stellen de dikke verbindingslijnen covalente bindingen voor. De hoek tussen die covalente bindingen wordt de bindingshoek genoemd.
g. Hoe groot zijn de bindingshoeken in een plátte 4-omringing?
2.2 In de vorige opdracht is vanwege het aantal
isomeren bij de molecuulformule CH2Cl2 gekozen voor een
tetraëderstructuur waarbij het C-atoom als centraal deeltje omringd wordt door
vier deeltjes.
Ook als je redeneert vanuit Lewisstructuren kom je uit op een zo groot
mogelijke bindingshoek, want de covalente bindingen worden daarin immers
gevormd door elektronenparen en die stoten elkaar vanwege hun negatieve lading
(van 2–) af.
a. Zoek in BINAS-tabel 53B op hoe groot de bindingshoeken zijn bij methaan en tetrachloormethaan.
Bij mono-, di- en trichloormethaan zijn de bindingshoeken wel ongeveer maar niet precies gelijk aan de wiskundig te berekenen hoek van a.
b. Hoe zou je met het Lewisstructuurmodel kunnen verklaren dat bij methaan en tetrachloormethaan de bindingshoeken wel precies gelijk zijn aan de theoretisch berekende waarde en bij mono-, di- en trichloormethaan niet?
Uit TUE vwo-scheikunde module 13:
2.1 In dit practicum leer je hoe je door uitbreiding en aanpassing van het deeltjesmodel op microniveau kunt verklaren dat er van octaan-2-ol wél en van octaan-1-ol géén enantiomeren bestaan.
a. Noem een eigenschap op macroniveau waarin twee enantiomeren van elkaar verschillen
Je hebt een dergelijke actie al eerder zien plaatsvinden: er werden structuurformules geïntroduceerd toen bij dezelfde molecuulformule
verschillende stoffen bleken te bestaan. Daardoor kon per stof één structuurformule worden toegekend. Omgekeerd kon uit het aantal mogelijke structuurformules het aantal isomeren bij een molecuul-formule afgeleid worden.
b. Geef de structuurformule en de naam van alle isomeren met de molecuulformule C3H8O.
Aan de structuurformules kun je niet zien dat er bij geen van de isomeren van vraag b sprake is van enantiomeren maar dat kan wel als je er ruimtelijke structuren bij betrekt.
In de volgende opdracht ga je dat doen voor octaan-1-ol en octaan-2-ol.
Ter voorbereiding daarop komen de papieren tetraeders van pas die je gemaakt hebt in opdracht 2.1 van module 12.
Kleur met een viltstift één van de topjes van de tetraeder rood, eentje blauw, eentje groen en eentje geel.
Vergelijk jouw gekleurde tetraeder met zoveel mogelijk gekleurde tetraeders van je klasgenoten.
Verdeel ze in zoveel groepen als er verschillende tetraeders zijn.
c. Hoeveel verschillende groepen zijn er?
Controleer m.b.v. een spiegel dat het spiegelbeeld van een tetraeder uit de ene groep gelijk is aan de tetraeders uit de andere groep.
d. Klopt het?
Schoenen en handschoenen zijn voorbeelden uit het
dagelijks leven van structuren die, net zoals de tetraeders
met vier kleuren, wel elkaars spiegelbeeld zijn maar niet identiek.
Even oefenen met “spiegelbeeld” en “wel of niet identiek”:
e. Is het spiegelbeeld van een veiligheidsbril identiek met het origineel?
f. Is het spiegelbeeld van een maatcilinder identiek met het origineel?
g. Is het spiegelbeeld van een schroef identiek met het origineel?
h. Is het spiegelbeeld van een kurkentrekker identiek met het origineel?
i. Is het spiegelbeeld van een tetraeder met twee rode, een blauwe en een gele top identiek met het origineel?
Bovenstaande vragen kunnen beantwoord worden door na te gaan
of de structuren wel of niet een inwendig spiegelvlak hebben. Zo
heeft een maatcilinder (als je tenminste niet let op de tekst) een inwendig spiegelvlak door het schenktuitje loodrecht naar beneden, en dan is het spiegelbeeld identiek aan het origineel.
Bij een schroef en een kurkentrekker kun je geen inwendig spiegel-vlak aanwijzen, bij een veiligheidsbril en de tetraeder van vraag i wel.
h. Klopt dat met je antwoorden op de vragen e t/m i?
In de volgende opdracht ga je “spiegelbeeld” en “wel of niet identiek” toepassen op ruimtelijke structuren waarmee octaan-1-ol en octaan-2-ol kunnen worden voorgesteld.
Uit TUE vwo-scheikundemodule 13:
2A.1 Vervolg van opdracht 1A.4 ….... Pasteur trok z'n conclusies!
Pasteur concludeerde uit zijn experimenten dat, als de kristallen die elkaars spiegelbeeld zijn, gelijke chemische en fysische eigenschappen hebben, behalve de draaiingshoek van gepolariseerd licht in oplossing, ook de moleculen van de links- en rechtsdraaiende stof elkaars spiegelbeeld moesten zijn.
Hij heeft dit idee niet verder modelmatig uitgewerkt. Dat deed onge-
veer vijfentwintig jaar later Van 't Hoff. Deze Leidse hoogleraar had
het tetraëdermodel ontworpen: een model dat in overeenstemming
is met de gegevens dat er slechts één monochloormethaan te vinden is en ook maar één dichloormethaan. (Dit model zou nog weer later ook in overeenstemming blijken te zijn met de bindingshoeken die voorspeld kunnen worden op basis van Lewisstructuren waarin vier elektronenparen van uit een centrum zover mogelijk van elkaar liggen, d.w.z. gericht naar de hoekpunten van een tetraëder.)
 Om
steun te zoeken voor zijn
Om
steun te zoeken voor zijn
theorie stuurde Van 't Hoff niet
alleen zijn op schrift gezette be-
vindingen maar ook kartonnen
modellen (zoals hiernaast afge-
beeld) naar bekende Europese
chemici.
In het Museum Boerhaave in
Leiden kun je de kartonnen tetra-
edertjes, die Van 't Hoff in 1875
plakte voor zijn studievriend
Bremer t.b.v. diens proefschrift,
in het echt bekijken.
De theorie van Van ’t Hoff is nog steeds actueel. Misschien heb je wel eens gehoord van linksdraaiende yoghurt? En de (bij)werking van sommige medicijnen berust op het feit dat er van een stof soms spiegelbeeldisomeren bestaan.
Lees daarover onder andere daarover in bron 41 het tweede deel van het artikel “Het leven is soms links, soms rechts”.